Radha, an aspiring landscape designer, is tasked with creating a visually captivating pool design that incorporates a unique arrangement of fountains. The challenge entails arranging the fountains in such a way that when water is thrown upwards, it forms the shape of a parabola. The graph of one such parabola is given below.
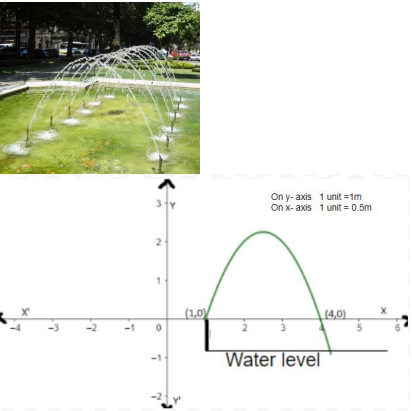
The height of each fountain rod above water level is 10 cm. The equation of the downward-facing parabola representing the water fountain is given by p(x) = −x2 + 5x − 4.
Based on the above information, answer the following questions:
(i) Find the zeroes of the polynomial p(x) from the graph.
(ii) Find the value of x at which water attains maximum height.
(iii) (A) If h is the maximum height attained by the water stream from the water level of the pool, then find the value of h.
OR
(B) At what point(s) on x-axis, the height of water above x-axis is 2 m?